Đáp án đề thi cao đẳng môn toán khối B năm 2013

Cùng với các khối A, A1, C, D sáng 15.7 các sĩ tử khối B sẽ làm bài thi môn toán tự luận trong 180 phút. Đối với môn Toán hay bất cứ môn thi nào thì thí sinh cũng nên làm các câu câu hỏi từ dễ đến khó, tùy theo sở trường của mình. Mỗi câu dễ, tính toán đơn giản cần được làm trong khoảng thời gian ngắn hơn 18 phút, dưới 15 phút là hợp lí nhất.

Tuyensinh247 sẽ liên tục cập đáp án ngay khi kết thúc môn thi.

Ngay khi ra khỏi phòng thi, Đáp án đề thi cao đẳng môn toán khối B sẽ được cập nhật nhanh và chính xác nhất trên tuyensinh247.com. Cụ thể:

Đáp án tham khảo: 10h15

Đáp án từ thầy cô giáo bộ môn: 11h-12h

Đáp án bộ GD&ĐT: Chiều ngày 16/7/2013

Ghi chú:

1. Đáp án tham khảo: Đáp án do Ban Tuyensinh247 đưa ra và đáp án của các bạn học sinh chia sẻ có ngay sau khi hết thời gian làm bài thi Môn toán.
2. Đáp án thầy cô: Đáp án sẽ được cập nhật từ tổ chuyên gia, thầy cô giáo bộ Môn toán sau 1h - 2h sau khi kết thúc môn thi.
3. Đáp án của bộ GD&ĐT: Cập nhật vào chiều tối ngày 16/7/2013

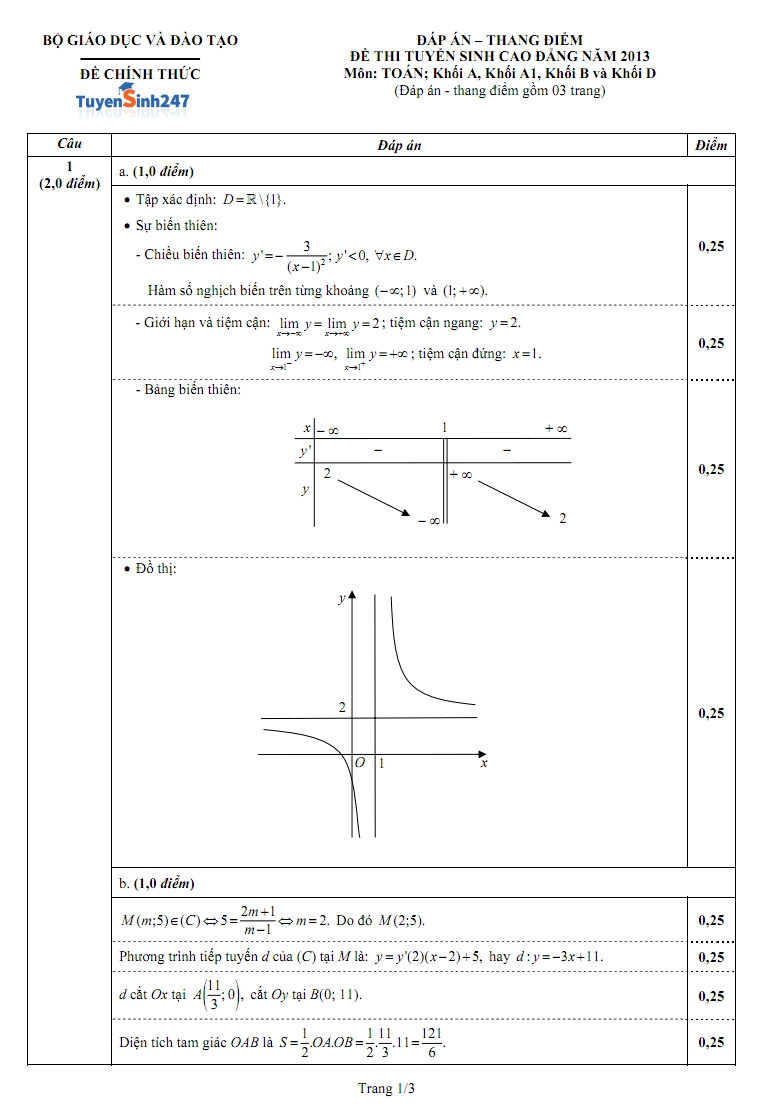
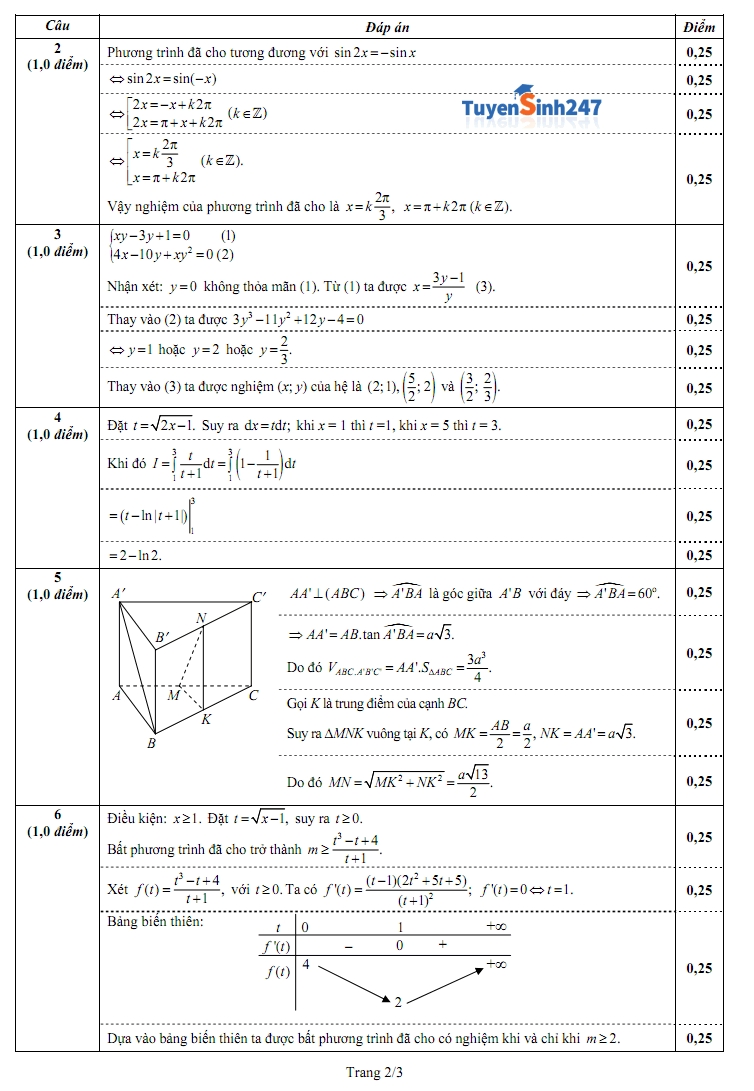
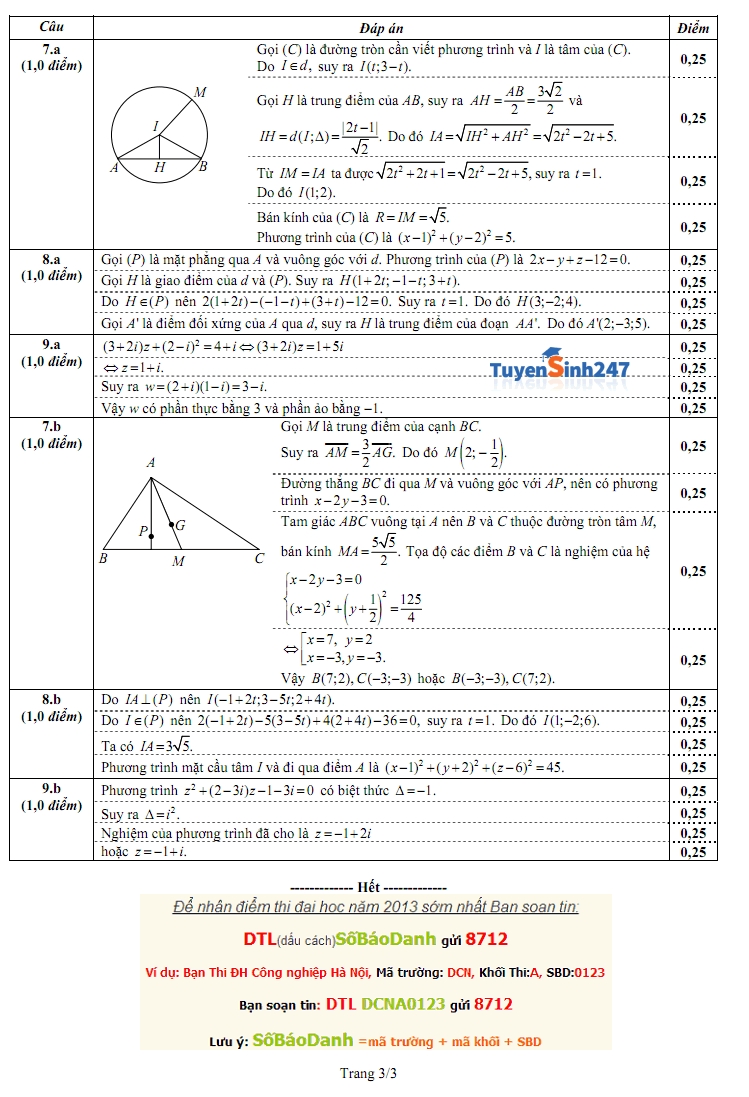
Đề thi cao đẳng môn toán khối B năm 2013

Đáp án đề thi cao đẳng môn toán khối B năm 2013 của bộ giáo dục

Cấu trúc đề thi cao đẳng môn Toán 2013 khá giống những năm gần đây. Trong đó:

Câu I (2 điểm): thường được chia thành hai câu nhỏ.

Câu 1: yêu cầu khảo sát và vẽ đồ thị của hàm số. Thí sinh cần lưu ý các kiến thức về đạo hàm, khảo sát dấu đạo hàm, đường tiệm cận…

Câu 2: thường yêu cầu tìm giá trị m (có liên quan đến đồ thị hàm số trên). Thí sinh phải dựa vào tính chất đồ thị và kết hợp với kiến thức hình học, tiếp tuyến, kiến thức tổng hợp về tổng, tích,… để làm câu này (lưu  ý: nếu học sinh không tìm thấy hướng giải thì hãy vẽ hình phát họa của câu hỏi và dựa trên đó sẽ tìm được lời giải).

Câu II (2 điểm): thường có hai câu nhỏ. Trong đó câu 1 thường là giải phương trình lượng giác. Câu 2 hay có dạng giải phương trình (hoặc bất phương trình) hay hệ phương trình đại số (thường là hai ẩn x, y). Thí sinh cần biết đặt các ẩn phụ để đưa bài toán trở về đơn giản hơn (khi gặp bài toán có dạng tổng – tích hoặc có cụm giống nhau), biến đổi các hằng đẳng thức đáng nhớ, thậm chí có đề phải dùng đến bất đẳng thức Cauchy để giải.

Câu III (1 điểm): thường là câu hỏi tính tích phân xác định (Lưu ý sau khi làm xong câu này, thí sinh nên dùng máy tính để kiểm tra kết quả. Nếu thấy kết quả khác phải xem lại cách tính của mình).

Câu IV (1 điểm): là câu hình học không gian thuần túy, thí sinh cần nắm vững các định lý về quan hệ song song, quan hệ vuông góc, các thủ thuật tính góc và khoảng cách, các công thức thể tích khối đa diện trong hình không gian (cần quan tâm và làm nhiều bài tập cho đến khi cảm thấy tự tin ở các dạng được in đậm vì các phần này luôn có trong đề khi ra thi)

Câu V (1 điểm): là câu khó nhất trong phần chung cũng như khó nhất trong cả đề thi. Thường là dạng chứng minh bất đẳng thức có điều kiện về đẳng thức hay bất đẳng thức hay tìm max, min của một biểu thức, hay max, min của một hàm số. Thí sinh cần sử dụng thành thạo và biến đổi nhuần nhuyễn các bất đẳng thức như Cauchy và cả bất đẳng thức tam giác, các điều kiện khi các bất đẳng thức xảy ra đẳng thức.

Câu VI.a (1 điểm): là câu hình học giải tích phẳng, đòi hỏi thí sinh phải nắm vững các kiến thức hình học thuần túy khá chắc, cộng với kỹ năng đặt tham số đúng sẽ làm đơn giản phần tính toán, nếu không phần tính toán sẽ rắc rối, phức tạp ( có thể tham khảo các bài giảng của thầy Đổng Quang Anh tại trung tâm luyện thi Nguồn Sáng Việt).

Đối với câu VI.b. (1 điểm): là câu hình học giải tích không gian, đòi hỏi thí sinh phải nắm vững các kiến thức về phương trình mặt phẳng, đường thẳng, khoảng cách từ một điểm đến mặt phẳng, hay đường thẳng, cách xác định tâm và bán kính mặt cầu.

Cuối cùng, câu VII (1 điểm): là câu số phức (có mặt trong hai năm trở lại đây). Thí sinh cần nắm vững công thức đại số, lượng giác và công thức Moivre trong số phức, đôi khi bài toán số phức được đưa về bài toán hình giải tích trong mặt phẳng. Cũng có thể là câu thuộc giải phương trình, hay hệ phương trình hàm log hay hàm mũ hoặc có thể là câu giải tích tổ hợp (không có mặt trong hai năm trở lại đây).

Thí sinh cần nắm vững biến đổi các công thức tổ hợp, chỉnh hợp, lấy tích phân và đạo hàm trong khai triển công thức nhị thức Newton.

Với cấu trúc một đề thi gồm các câu với mức độ phức tạp tương ứng như trên, thí sinh nên ưu tiên làm các câu từ dễ tới khó và phù hợp với sở trường của mình.

Theo Thethaohangngay