Đề thi vào lớp 10 môn Toán Thanh Hóa năm 2014Đề thi tuyển sinh vào lớp 10 tỉnh Thanh Hóa môn Toán năm 2014 có đáp án được cập nhật thứ hai ngày 30/6/2014, các em tham khảo dưới đây. Đề thi tuyển sinh 10 môn Toán tỉnh Thanh Hóa năm 2014 - Đề ASỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT TỈNH THANH HÓA Năm học 2014 – 2015 ĐỀ CHÍNH THỨC MÔN THI: Toán Đề A Ngày thi: 30 tháng 6 năm 2014 Câu 1: (2,0 điểm)
a. x – 2 = 0 b. x2 – 6x + 5 = 0
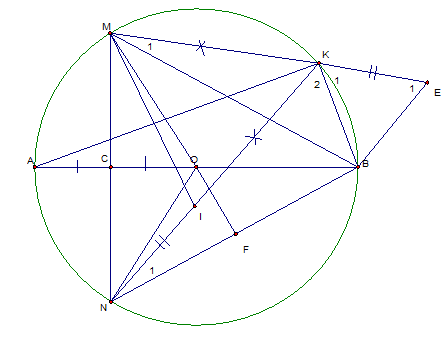
1. Rút gọn A. 2. Tính giá trị của biểu thức A khi x = 4 + 2√3 Câu 3: (2,0 điểm) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): tham số m và Parabol (P): y = x2. 1. Tìm m để đường thẳng (d) đi qua điểm A(1; 0). 2. Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt có hoàng độ lần lượt là x1, x2 thỏa mãn |x1 = x2| = 2 Câu 4: (3,0 điểm) Cho đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm của OA; qua C kẻ đường thẳng vuông góc với OA cắt đường tròn đó tại hai điểm phân biệt M và N. Trên cung nhỏ BM lấy điểm K ( K khác B và M), trên tia KN lấy điểm I sao cho KI = KM. Gọi H là giao điểm của AK và MN. Chứng minh rằng: 1. Tứ giác BCHK là tứ giác nội tiếp. 2. AK.AH = R2 3. NI = BK Câu 5: (1,0 điểm) Cho các số thực dương x, y, z thỏa mãn xyz = 1. Tìm giá trị lớn nhất của biểu thức Đáp án đề thi tuyển sinh 10 môn Toán tỉnh Thanh Hóa năm 2014 - Đề ANguồn đáp án GV Nguyễn Xuân Chiến |
-
Sáng 30/6, gần 35 nghìn thí sinh thi vào lớp 10 Thanh Hóa
Kỳ thi tuyển sinh vào lớp 10 năm 2014 tại Thanh Hóa đã bắt đầu diễn ra vào sáng 30/6 với môn thi Toán, có gần 35.000 thí sinh dự thi trong kỳ thi tuyển lớp 10 này.
-
Đề minh họa vào lớp 10 môn Lịch sử và Địa lý 2025 - Ninh Bình
Đề minh họa vào lớp 10 năm học 2025 - 2026 môn Lịch sử và Địa lý đã được Sở GD và ĐT Ninh Bình công bố. Đề minh họa gồm có 50 câu với 7 trang cụ thể như sau:
-
Đề minh họa vào lớp 10 môn KHTN 2025 Sở GD Ninh Bình
Tham khảo đề minh họa vào lớp 10 năm 2025 môn khoa học tự nhiên (Hóa, Sinh, Anh) của Sở GD và ĐT Ninh Bình được đăng tải dưới đây.
-
Đề minh họa vào lớp 10 môn Anh 2025 - Ninh Bình
Đề minh họa vào lớp 10 năm học 2025 - 2026 của Sở GD và ĐT Ninh Bình đã được công bố. Đề thi gồm 5 phần tương ứng với 7 trang như sau:
-
Đề minh họa môn Văn vào lớp 10 - Ninh Bình 2025
Đề minh họa vào lớp 10 năm 2025 môn Ngữ Văn của Sở GD và ĐT Ninh Bình đã được công bố với 2 dạng đề. Đề thi gồm 2 phần như sau:

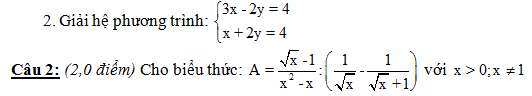
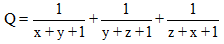

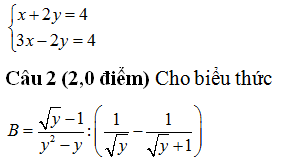
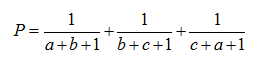 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức