Đề thi thử đánh giá tư duy Bách khoa số 6 - Tuyensinh247 (Có đáp án)

CẤU TRÚC BÀI THI ĐÁNH GIÁ TƯ DUY ĐẠI HỌC BÁCH KHOA HÀ NỘI NĂM 2024

Biên soạn: Ban chuyên môn Tuyensinh247.com 

PHẦN I: TƯ DUY TOÁN HỌC

Câu 1: Gieo con xúc xắc 100 lần, kết quả thu được ghi ở bảng sau:

Xác suất của biến cố mặt lẻ chấm xuất hiện bằng

A. \(\dfrac{{21}}{{50}}\).  B. \(\dfrac{{11}}{{25}}\). 

C. \(\dfrac{{14}}{{25}}\).  D. \(\dfrac{{29}}{{50}}\).

Câu 2: Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Trong mặt phẳng tọa độ Oxy, gọi \((H)\) là tập hợp điểm biểu diễn số phức \(w = (1 + \sqrt 3 i)z + 2\) thỏa mãn \(|z - 1| \le 2\). Hình \((H)\) là một_________có bán kính là _________ và có diện tích bằng _________.

Câu 3: Cho hình nón có thiết diện qua trục là tam giác đều. Gọi V₁, V₂ lần lượt là thể tích của khối cầu ngoại tiếp và nội tiếp hình nón đã cho. Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\).

     A. 16.                    B. 8.                         C. 2.                         D. 4. 

Câu 4: Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng \(a\) và \(SA \bot (ABCD)\). Biết \(SA = \dfrac{{a\sqrt 6 }}{3}\). Tính góc giữa SC và \((ABCD)\).

     A. 30°.                  B. 45°.                   C. 60°.              D. 20°.                      

Câu 5: Cho hàm số \(y = f(x)\) xác định và có đạo hàm trên \(\mathbb{R}\), biết \(f(4) = 5\) và \({f^\prime }(4) = 2\). Giới hạn \(\mathop {\lim }\limits_{x \to 4} \dfrac{{{f^2}(x) + f(x) - 30}}{{\sqrt x  - 2}}\) bằng  _________. 

Câu 6: Theo thống kê tại một nhà máy Z, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là \(P(x) = \dfrac{{95{x^2} + 120x}}{4}\), với x là thời gian làm việc trong một tuần. Nhà máy cần áp dụng thời gian làm việc mỗi tuần _______  giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất. 

Câu 7: Trong không gian Oxyz, cho ba điểm \(A(1;0;0),B(2;0;1),C(1;1;1)\) và mặt phẳng \((P):x + y + z - 6 = 0\). Gọi \((S)\) là mặt cầu đi qua ba điểm A, B, C và có tâm thuộc mặt phẳng \((P)\).

Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Bán kính mặt cầu (S) bằng _______

Tâm mặt cầu (S) có tung độ bằng _______; cao độ bằng _______. 

Câu 8: Phần nguyên của số thực x là số nguyên lớn nhất không vượt quá x, kí hiệu là [x]. Chẳng hạn [1,2]=1; [-2;7]= -3.

Tổng các phần nguyên của số \(\sqrt k \) với k là số tự nhiên và  k ∈ [1;24] bằng

     A. 70.                   B. 64.                     C. 76.                      D. 82. 

Câu 9: Tìm tham số thực \(m\) để hàm số \(y = f(x) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{{x^2} + x - 12}}{{x + 4}}}&{{\rm{khi }}x \ne  - 4}\\{mx + 1}&{{\rm{khi }}x =  - 4}\end{array}} \right.\) liên tục tại điểm \({x_0} =  - 4\).

     A. \(m = 4\).       B. \(m = 3\).            C. \(m = 2\).           D. \(m = 5\).

Câu 10: Có 4 hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn ngẫu nhiên một toa. Tính xác suất để 1 toa có 3 người, 1 toa có 1 người, 2 toa còn lại không có ai.

 A. \(\dfrac{3}{4}\)     B. \(\dfrac{3}{{16}}\)   

 C. \(\dfrac{{13}}{{16}}\)   D. \(\dfrac{1}{4}\) 

Câu 11: Trong không gian Oxyz, cho mặt cầu \((S):{(x - 3)^2} + {(y - 1)^2} + {(z - 1)^2} = 4\) và ba điểm \(A( - 1;2; - 3),B(5;2;3),C(1;2;3)\). Gọi \(S\) là điểm thay đổi trên mặt cầu \((S)\). Giá trị lớn nhất của thể tích khối chóp S.ABC là _________. 

Câu 12: Cho hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a.

Mỗi phát biểu sau đây là đúng hay sai?

 Câu 13: Cho hàm số \(f(x) = \dfrac{{x - m}}{{x + 4}}\). Tổng tất cả các giá trị của  m  để \(\mathop {\min }\limits_{[ - 3;3]} f(x) = 2\) là     A. 0.                            B. −11.                 C. −16.          D. 1. 

Câu 14: Tích phân \(I = \int\limits_1^2 {\dfrac{1}{{2x - 1}}} \;{\rm{d}}x\) bằng

     A. \(I = \ln 3 - 1\).                                                        B. \(I = \ln \sqrt 3 \).

     C. \(I = \ln 2 + 1\).                                                       D. \(I = \ln 2 - 1\). 

Câu 15: Cho \(\log _2^2(xy) = {\log _2}\left( {\dfrac{x}{4}} \right){\log _2}(4y)\). Biểu thức \(P = {\log _3}(x + 4y + 4) + {\log _2}(x - 4y - 1)\) có giá trị bằng

     A. 3.                                                                             B. 2.

     C. \(\ln \dfrac{3}{2}\).                                                 D. \({\log _3}6 + 1\). 

Câu 16: Cho hình phẳng (H) giới hạn bởi đồ thị hai hàm số \(y = 2{x^2}\) và \(y = x\).

Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Đồ thị hai hàm số cắt nhau tại điểm có hoành độ bằng ______.

Diện tích hình phẳng (H) bằng ______. 

Câu 17: Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \({f^\prime }(x) = {x^2}(x + 2)(x - 3)\).

Mỗi phát biểu sau đây là đúng hay sai?

 Câu 18: Có bao nhiêu số tự nhiên có 3 chữ số có dạng \(\overline {abc} \) thỏa mãn \(a,\,\,b,\,\,c\) là độ dài 3 cạnh của một tam giác cân?

     A. 106.                    B. 165.                     C. 45.                      D. 61. 

Câu 19: Trong không gian, cho bốn mặt cầu có bán kính lần lượt là 2,3,3,2 tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng

     A. \(\dfrac{5}{9}\).            B. \(\dfrac{3}{7}\).           

     C. \(\dfrac{7}{{15}}\).       D. \(\dfrac{6}{{11}}\). 

Câu 20: Để in một quyển tạp chí, người ta cần sử dụng 1 tờ giấy bìa cứng và 25 tờ giấy in cùng với mực in. Một tập giấy in gồm 500 tờ và một tập giấy bìa cứng gồm 60 tờ, có giá gấp đôi giá của một tập giấy in. Mỗi hộp mực in được 130 tờ giấy in hoặc giấy bìa cứng. Một tập giấy in có giá 50 nghìn đồng. Hộp mực có giá 900 nghìn đồng mỗi hộp.

Với ngân sách là 60 triệu đồng, có tối đa  ______ tạp chí hoàn chỉnh có thể được in.

Câu 21: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 3\sin x + 4\cos x + 1\) bằng ______. 

Câu 22: Xét các số thực dương \(a,b\) thoả mãn \({\log _2}\dfrac{{1 - ab}}{{a + b}} = 2ab + a + b - 3\).

Mỗi phát biểu sau đây là đúng hay sai? 

Câu 23: Một vật đang chuyển động đều với vận tốc v0(m/s)  thì bắt đầu tăng tốc với phương trình gia tốc \(a(t) = {v_0}t + {t^2}\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\) trong đó t là khoảng thời gian được tính bằng giây kể từ thời điểm vật bắt đầu tăng tốc. Biết quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100 m. Khi đó, vận tốc ban đầu v0 của vật bằng bao nhiêu (làm tròn đến chữ số thập phân thứ 3)?

     A. 20,722 (m/s).                                                         B. 12,433 (m/s)

     C. 21,722 (m/s).                                                         D. 13,433 (m/s).

Câu 24: Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có cạnh bên bằng \(a\sqrt 2 \), đáy ABC là tam giác vuông tại \(B,BC = a\sqrt 3 ,AB = a\). Biết hình chiếu vuông góc của đỉnh \(A'\) lên mặt đáy là điểm \(M\) thoả mãn \(3\overrightarrow {AM}  = \overrightarrow {AC} \). Thể tích lăng trụ tam giác \(ABC.A'B'C'\) bằng

     A. \(\dfrac{{{a^3}\sqrt 7 }}{2}\)                                B. \(\dfrac{{{a^3}\sqrt 7 }}{6}\)  C. \(\dfrac{{{a^3}\sqrt {42} }}{2}\).                                    D. \(\dfrac{{{a^3}\sqrt {42} }}{6}\)

Câu 25: Mỗi phát biểu sau là đúng hay sai? 

Câu 26: Cho số phức z thỏa mãn \({z^2} + z.\bar z - 1 = 0\).

Mỗi phát biểu sau đây là đúng hay sai?

Câu 27: Hai chất điểm \(M\) và \(N\) chuyển động thẳng đều trên trục Ox và Oy vuông góc với nhau (như hình vẽ):

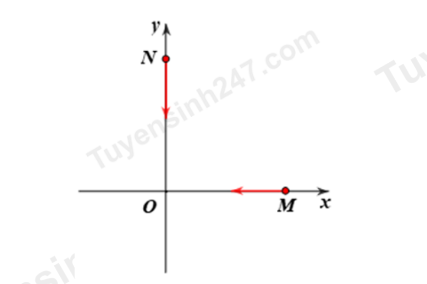
Tại thời điểm t = 0 chất điểm \(M\) đang cách gốc tọa độ \(O\) một đoạn 10 mét; chất điểm \(N\) cách gốc tọa độ \(O\) một đoạn \(12\;{\rm{m}}\). Hai chất điểm cùng chuyển động hướng về \(O\) với các tốc độ tương ứng là 0,4 m/s và 0,3 m/s. Khoảng cách nhỏ nhất giữa 2 chất điểm bằng bao nhiêu?

     A. 1,2 m.          B. 3,6 m.                           C. 12,96 m.                  D. 3,4 m.

Câu 28: Một quả bóng được ném theo phương ngang xác định bởi phương trình \(s = \dfrac{2}{3}{t^3} - \dfrac{5}{2}{t^2} - 3t + 2\), trong đó \(t\) tính bằng giây, \(s\) tính bằng mét. Tính gia tốc của quả bóng tại thời điểm vận tốc triệt tiêu.     

A. \(a = 3\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\).                                          

B. \(a = 6\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\).     

C. \(a = 5\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\).                                          

D. \(a = 7\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\).

Câu 29: Cho tứ diện đều cạnh \(a\) và điểm \(I\) bất kì nằm trong tứ diện. Tổng khoảng cách từ \(I\) đến các mặt của tứ diện bằng

     A. \(\dfrac{a}{{\sqrt 5 }}\).                        B. \(\dfrac{{a\sqrt 6 }}{3}\).       

 C. \(\dfrac{{a\sqrt 5 }}{6}\).                 D. \(\dfrac{{a\sqrt 3 }}{4}\).

Câu 30: Một loại nút chai rượu được sản xuất bằng cách cắt bỏ đi một góc của khúc gỗ hình trụ có chiều cao 3 cm, đường kính đáy 1,6 cm bằng một mặt phẳng như hình vẽ, biết AB = 0,8 cm. Sau đó bề mặt cắt sẽ được sơn bằng một loại sơn không độc hại. Nếu sản xuất 100 000 nút chai rượu như thế thì cần bao nhiêu lít sơn không độc hại kể trên (biết rằng 1 lít sơn được 5cm²)? 

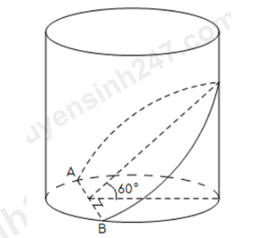
     A. 2,7 lít.                 B. 7,8 lít.                    C. 5,4 lít.                   D. 3,9 lít. 

Câu 31: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({d_1}:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = t}\\{z = 7}\end{array}} \right.\) và  \({d_2}:\left\{ {\begin{array}{*{20}{l}}{x = 6 + t}\\{y = 9 - mt}\\{z = 1 - (m + 1)t}\end{array}} \right.\). Giá trị của tham số m để hai đường thẳng d₁ và d₂ vuông góc với nhau là

     A. −2.                 B. 1.                         C. −1.                   D. 0. 

Câu 32: Cho dãy số \(\left( {{u_n}} \right):\left\{ {\begin{array}{*{20}{c}}{{u_1} = 2}\\{{u_{n + 1}} + 4{u_n} = 4 - 5n}\end{array}} \right.\) với \(n \ge 1\). Giá trị của \({u_{2023}} - 2{u_{2022}}\) bằng

     A. \(2018 - {3.4^{2021}}\).                       B. \(2020 + {3.4^{2022}}\).

     C. \(2020 - {3.4^{2021}}\).                     D. \(2018 + {3.4^{2022}}\). 

Câu 33: Một công ty du lịch đầu tư xây dựng 24 nhà chòi trong khu du lịch sinh thái. Mô hình thiết kế như hình vẽ, mái nhà có hình dạng là mặt xung quanh của hình nón với bán kính đáy là 3m và chiều cao của mái nhà là 4m. Chi phí làm mái là 2 triệu đồng/m², chi phí làm hệ thống cột, khung nhà và nền nhà là 100 triệu đồng/nhà chòi. Công ty chỉ trả được 30% tổng chi phí xây dựng 24 nhà chòi đó. Số tiền còn thiếu, công ty phải vay ngân hàng với lãi suất 10%/năm (với thể thức lãi kép, lãi suất không thay đổi trong thời gian vay). Sau đúng 5 năm, công ty trả nợ ngân hàng cả gốc và lãi với số tiền là (làm tròn đến hàng ngàn) 

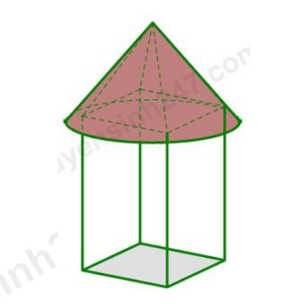
     A. 3 456 123 000 đồng.                                            B. 5 255 678 000 đồng.

     C. 7 508 112 000 đồng.                                            D. 2 252 434 000 đồng. 

Câu 34: Phương trình \({\log _2}\left( {{3^{{{\log }_6}x}} + x} \right) = \dfrac{1}{2}{\log _6}{x^2}\) có bao nhiêu nghiệm?             

     A. 1.                        B. 0.                          C. 2.                        D. 3. 

Câu 35: Với số nguyên dương \(n\), gọi \({a_{3n - 3}}\) là hệ số của \({x^{3n - 3}}\) trong khai triển thành đa thức của \({\left( {{x^2} + 1} \right)^n}{(x + 2)^n}\). Tìm \(n\) để \({a_{3n - 3}} = 26n\).

     A. \(n = 6\).              B. \(n = 7\).               C. \(n = 5\).           D. \(n = 4\). 

Câu 36: Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\backslash \{  - 1;2\} \), liên tục trên các khoảng xác định của nó và có bảng biến thiên như sau: 

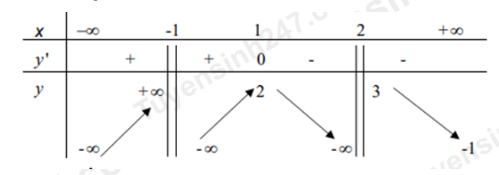
Chọn các khẳng định đúng.

Đồ thị hàm số \(y = \dfrac{1}{{f(x) - 2}}\) có

• o 3 đường tiệm cận ngang.
• o 5 đường tiệm cận.
• o 2 đường tiệm cận ngang.
• o 2 đường tiệm cận đứng.

Câu 37: Cho số phức \(z\) thỏa mãn \(|z - 6| + |z + 6| = 20\). Gọi M, n lần lượt là môđun lớn nhất và nhỏ nhất của z. Tính \(M - n\).

     A.  2.                                 B. 5.                 C. 8.                      D. 6. 

Câu 38: Một cốc nước dạng hình trụ có chiều cao 15 cm, đường kính đáy 4 cm, lượng nước trong cốc cao 10 cm. Thả vào cốc nước 3 viên đá hình cầu có đường kính 2 cm. (Bỏ qua độ dày của cốc).

Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Nước trong cốc dâng thêm ______  cm.

Nước dâng cao cách mép cốc ______ cm. 

Câu 39: Bà chủ quán trà sữa X  muốn trang trí quán cho đẹp nên quyết định thuê nhân công xây một bức tường bằng gạch với xi măng (như hình vẽ bên dưới), biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có ít hơn hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là bao nhiêu viên?

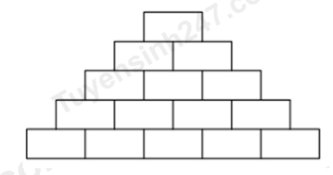
     A. 25250 viên.                                                            B. 250500 viên.

     C. 12550 viên.                                                            D. 125250 viên. 

Câu 40: Cho khối lăng trụ đứng \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có \(B{B^\prime } = a\), đáy ABC là tam giác vuông cân tại \(B\) và \(AC = a\sqrt 2 \). Tính thể tích \(V\) của khối lăng trụ đã cho.

     A. \(V = \dfrac{{{a^3}}}{6}\).                        B. \(V = \dfrac{{{a^3}}}{2}\).

     C. \(V = {a^3}\).                                      D. \(V = \dfrac{{{a^3}}}{3}\).

PHẦN II: TƯ DUY ĐỌC HIỂU 

“Nhận” và “cho” trong hội nhập văn hóa 

[1] (TN&MT) - Từ cuối thập niên 80 của thế kỷ trước, Ủy ban văn hóa, giáo dục của Liên hợp quốc (UNESCO) đã khuyến cáo: Bước sang thế kỷ 21, nền khoa học của nhân loại có những bước tiến như vũ bão, làm đảo lộn nhiều giá trị tưởng như đã ổn định. Những thành tựu kì diệu của khoa học, công nghệ... sẽ kéo theo những thay đổi về văn hóa, tác động sâu sắc đến các giá trị văn hóa truyền thống theo hướng tích cực hoặc tiêu cực.

Vì vậy, các dân tộc cần chuẩn bị cho quá trình hội nhập một cách thông minh, trên cơ sở bảo tồn vững chắc những tinh hoa truyền thống của nền văn hóa dân tộc mình, góp phần làm phong phú nền văn hóa chung của nhân loại. 

[2] Từ trước tới nay, Đảng ta luôn luôn đề cao vai trò của văn hóa trong sự nghiệp đấu tranh giải phóng dân tộc, xây dựng và bảo vệ Tổ quốc. Trong sự nghiệp đổi mới, Đảng xác định văn hóa là động lực và nền tảng của phát triển bền vững, “Xây dựng văn hóa trong chính trị và kinh tế” là cốt lõi của “Văn hóa hội nhập” Việt Nam trong thời kỳ hội nhập và toàn cầu hóa, vì văn hóa không đứng ngoài chính trị và kinh tế. Hội nhập văn hóa đồng thời diễn ra trong quá trình hội nhập kinh tế.

[3] Nếu hội nhập kinh tế diễn ra theo xu hướng hòa đồng các giá trị thì hội nhập văn hóa - vấn đề cốt tử là phải bảo tồn cho được các giá trị riêng biệt, đó chính là bản sắc văn hóa của dân tộc. Hội nhập văn hóa là sự thống nhất giữa “nhận” và “cho”. “Nhận” cái mới của nước ngoài và “cho” thế giới, đóng góp cho thế giới những điều đặc sắc của văn hóa Việt Nam. Tức là, quá trình hội nhập, chúng ta không chỉ tiếp biến văn hóa nhân loại để làm giàu có thêm kho tàng văn hóa Việt Nam, mà văn hóa Việt Nam có thể đóng góp những giá trị đặc sắc của mình vào văn hóa chung của nhân loại. Văn hóa Việt Nam có đủ tầm vóc, bản lĩnh, tự tin để tham gia định hình những giá trị chung trong văn hóa của nhân loại. Đó là một nội dung quan trọng của tiến trình hội nhập văn hóa. 

[4] Giao lưu và hội nhập văn hóa có vai trò và ý nghĩa hết sức quan trọng đối với sự phát triển nền văn hóa của mỗi quốc gia, dân tộc. Nhưng hội nhập bao giờ cũng có 2 mặt. Mặt tích cực là giao lưu và hội nhập sẽ giúp cho văn hóa mỗi dân tộc luôn phát triển, tiếp nhận được những tinh hoa văn hóa của các dân tộc khác để bồi đắp thêm cho văn hóa của dân tộc mình, đồng thời, quảng bá được những giá trị văn hóa của dân tộc mình cho các dân tộc khác. Tuy nhiên, cùng với đó là nguy cơ “đồng hóa” các hệ giá trị, các chuẩn mực văn hóa dân tộc, đe dọa tính sáng tạo của các nền văn hóa dân tộc, dẫn đến tình trạng “vong bản”, thậm chí thủ tiêu các giá trị văn hóa dân tộc.

[5] Bản sắc văn hóa của một dân tộc chính là cốt cách của dân tộc ấy. Cốt cách dân tộc là những phẩm chất tương đối ổn định và bền vững, bởi nó được hình thành và tồn tại trong lịch sử tồn tại và phát triển của dân tộc. Đồng thời, cốt cách dân tộc được thể hiện rất rõ ở lĩnh vực văn hóa, làm nên bản sắc văn hóa của dân tộc. Vì vậy, giữ gìn bản sắc văn hóa dân tộc cũng chính là giữ gìn cốt cách của dân tộc. Một nền văn hóa giữ được cốt cách dân tộc sẽ là một nền văn hóa có đủ nội lực đề kháng, chống lại các cuộc "xâm lăng văn hóa" từ bên ngoài. Một nền văn hóa như vậy mới đủ tự tin và bản lĩnh để tiếp nhận chọn lọc những giá trị văn hóa của các dân tộc khác, "dân tộc hóa" những giá trị văn hóa nhân loại để đồng hành cùng nhân loại.

[6] Trong quá trình giao lưu văn hóa hiện nay, sự xâm nhập, thẩm thấu các giá trị văn hóa ngoại lai vào nước ta diễn ra thông qua nhiều hình thức, con đường rất tinh vi, thông qua các loại hình nghệ thuật phức hợp. Chưa kể, đang có những âm mưu “xâm lăng” văn hóa, làm mờ nhòe ranh giới, làm “mù nhận thức” của người tiếp nhận. Nguy cơ ấy đòi hỏi dân tộc ta phải trang bị cho nền văn hóa truyền thống một sức đề kháng đủ mạnh, để cốt cách văn hóa Việt Nam thẩm thấu và di truyền vào con tim, khối óc, huyết quản... của mỗi con dân nước Việt, để trong công cuộc hội nhập, văn hóa chỉ hòa nhập chứ không bị “hòa tan”.

                  (Theo nhà văn Mai Nam Thắng, baotainguyenmoitruong.vn, ngày 02/3/2023)

XEM TOÀN BỘ ĐỀ VÀ ĐÁP ÁN CHI TIẾT